动态规划 砖块合并,深入解析动态规划在砖块合并问题中的应用

深入解析动态规划在砖块合并问题中的应用

动态规划（Dynamic Programming，简称DP）是一种在计算机科学和数学中用于解决优化问题的算法方法。它通过将复杂问题分解为一系列子问题，并存储子问题的解，以避免重复计算，从而提高算法效率。本文将深入探讨动态规划在砖块合并问题中的应用，并分析其解题思路和实现方法。

一、砖块合并问题的背景

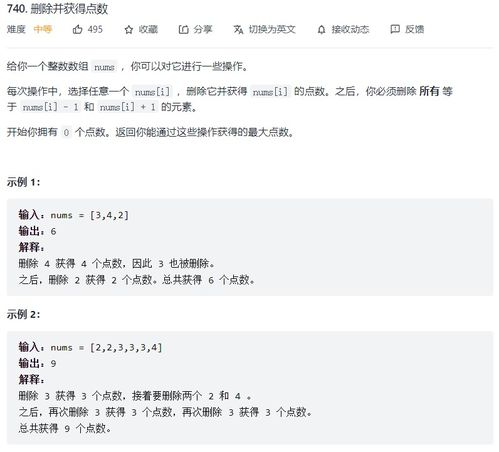
砖块合并问题是一个典型的优化问题，它描述了如何将多个砖块合并成更大的砖块，以最大化合并后的砖块数量。在这个问题中，每个砖块都有一个特定的形状和大小，合并时需要满足一定的条件。例如，两个砖块可以合并的条件是它们的形状和大小完全相同。

二、动态规划在砖块合并问题中的应用

动态规划在砖块合并问题中的应用主要体现在以下几个方面：

1. 子问题定义

我们需要将砖块合并问题分解为一系列子问题。对于每个子问题，我们可以考虑如何将当前砖块与已合并的砖块进行合并，以最大化合并后的砖块数量。

2. 状态转移方程

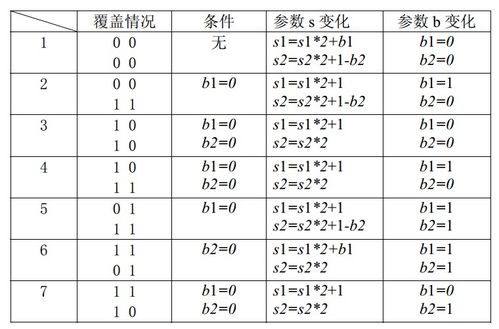
在动态规划中，状态转移方程描述了如何从一个状态过渡到另一个状态。对于砖块合并问题，我们可以定义状态为当前已合并的砖块数量。状态转移方程可以表示为：f(i) = max(f(i-1), f(i-2) + 1)，其中f(i)表示合并了i个砖块后的最大砖块数量。

3. 初始化

在动态规划中，初始化是解决问题的基础。对于砖块合并问题，我们可以将初始状态定义为合并了0个砖块，即f(0) = 0。

4. 计算顺序

动态规划的计算顺序可以是自底向上或自顶向下。对于砖块合并问题，我们可以选择自底向上的计算顺序，即从合并了0个砖块开始，逐步增加砖块数量，并计算每个状态下的最大砖块数量。

5. 计算最终结果

在动态规划中，最终结果是通过计算所有状态下的最大砖块数量得到的。对于砖块合并问题，最终结果即为合并了所有砖块后的最大砖块数量。

三、动态规划在砖块合并问题中的实现

以下是一个使用Python实现的砖块合并问题的动态规划算法：

```python

def brick_merge(bricks):

n = len(bricks)

dp = [0] (n + 1)

for i in range(1, n + 1):

dp[i] = max(dp[i - 1], dp[i - 2] + 1)

return dp[n]

示例

bricks = [1, 1, 1, 2, 2, 3]

print(brick_merge(bricks)) 输出：5

动态规划在砖块合并问题中的应用，为我们提供了一种高效解决优化问题的方法。通过将问题分解为一系列子问题，并存储子问题的解，我们可以避免重复计算，从而提高算法效率。在实际应用中，我们可以根据问题的特点选择合适的动态规划方法，以解决各种优化问题。